一、本章涉及到的专业名词和概念
卷积神经网络:含有卷积层的神经网络。
互相关运算:
二维卷积层:它有宽和高两个维度,常用来处理图像数据。将输入和卷积核做互相关运算,并加上一个标量偏差来得到输出。参数包括卷积核和标量偏差。
卷积运算:
二维卷积层
互相关运算和卷积运算的关系:为了得到卷积运算的输出,我们只需要将核数组左右翻转并上下翻转,再与输入数组做互相关运算。但是,再深度学习中核数组都是学出来的:卷积层无论使用互相关运算或卷积运算都不影响模型预测时的输出。
二、基本网络概念:
- 二维互相关运算实现代码
import torch from torch import nn def corr2d(X, K): # 本函数已保存在d2lzh_pytorch包中方便以后使用 h, w = K.shape Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1)) for i in range(Y.shape[0]): for j in range(Y.shape[1]): Y[i, j] = (X[i: i + h, j: j + w] * K).sum() return Y - 卷积核的作用:有效地表征局部空间
通过一个K = torch.tensor([[1, -1]])的卷积核,达到了检测物体边缘的作用。
原始数据X 为一个图像,中间4列为黑,其余为白
然后用K和X进行互运算,得到结果如下tensor([[1., 1., 0., 0., 0., 0., 1., 1.], [1., 1., 0., 0., 0., 0., 1., 1.], [1., 1., 0., 0., 0., 0., 1., 1.], [1., 1., 0., 0., 0., 0., 1., 1.], [1., 1., 0., 0., 0., 0., 1., 1.], [1., 1., 0., 0., 0., 0., 1., 1.]])
看到结果第2 6列为非0,其他列都是0,而这两列是X中黑白开始变化的那两列。tensor([[ 0., 1., 0., 0., 0., -1., 0.], [ 0., 1., 0., 0., 0., -1., 0.], [ 0., 1., 0., 0., 0., -1., 0.], [ 0., 1., 0., 0., 0., -1., 0.], [ 0., 1., 0., 0., 0., -1., 0.], [ 0., 1., 0., 0., 0., -1., 0.]]) - 填充和步幅
填充:在输入的高和宽的两侧增加元素,可以增大卷积运算的输出结果
步幅:增大卷积核每次滑动的间距,步幅可以减小输出的高和宽, 多输入通道和多输出通道
例如彩色图像在高和宽2个维度外还有RGB3个颜色通道。假设彩色图像的高和宽分别是h和w(像素),那么它可以表示为一个3hw的多维数组。我们将大小为3的这一维称为通道维。
输入数据含多个通道时,我们需要和输入数据通道的个数 相同通道数的卷积核。当通道数为3时,我们会为每个通道都分配一个形状一样的卷积核。在每一个通道上都做互相关运算,最后将结果相加,最后得到一个二维的输出。示例如下所示: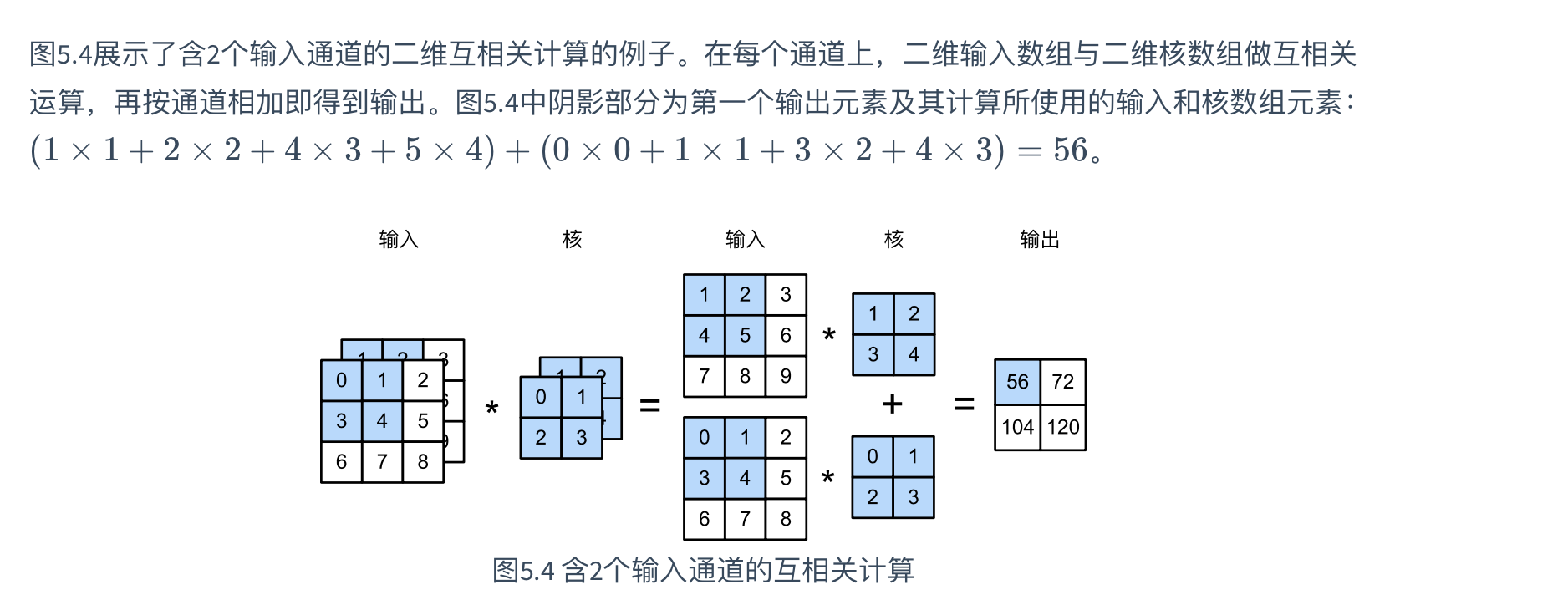
多输出通道:
1×1卷积层的作用与全连接层等价池化层
a. 为了缓解卷积层对位置的过度敏感性
b. 分为最大池化或平均池化
c. 同卷积层一样,池化层每次对输入数据的一个固定形状窗口(又称池化窗口)中的元素输出。不同于卷积层里计算输入和核的互相关性,池化层直接计算池化窗口内元素的最大值或者平均值。分别叫做最大池化或平均池化。
d. 池化层代码import torch from torch import nn def pool2d(X, pool_size, mode='max'): X = X.float() p_h, p_w = pool_size Y = torch.zeros(X.shape[0] - p_h + 1, X.shape[1] - p_w + 1) for i in range(Y.shape[0]): for j in range(Y.shape[1]): if mode == 'max': Y[i, j] = X[i: i + p_h, j: j + p_w].max() elif mode == 'avg': Y[i, j] = X[i: i + p_h, j: j + p_w].mean() return Ye. 多通道时,池化层对每个输入通道分别池化,而不是像卷积层那样将各个通道的输入相加.
三、典型卷积网络
- 卷积神经网络(LeNet)
- 网络结构
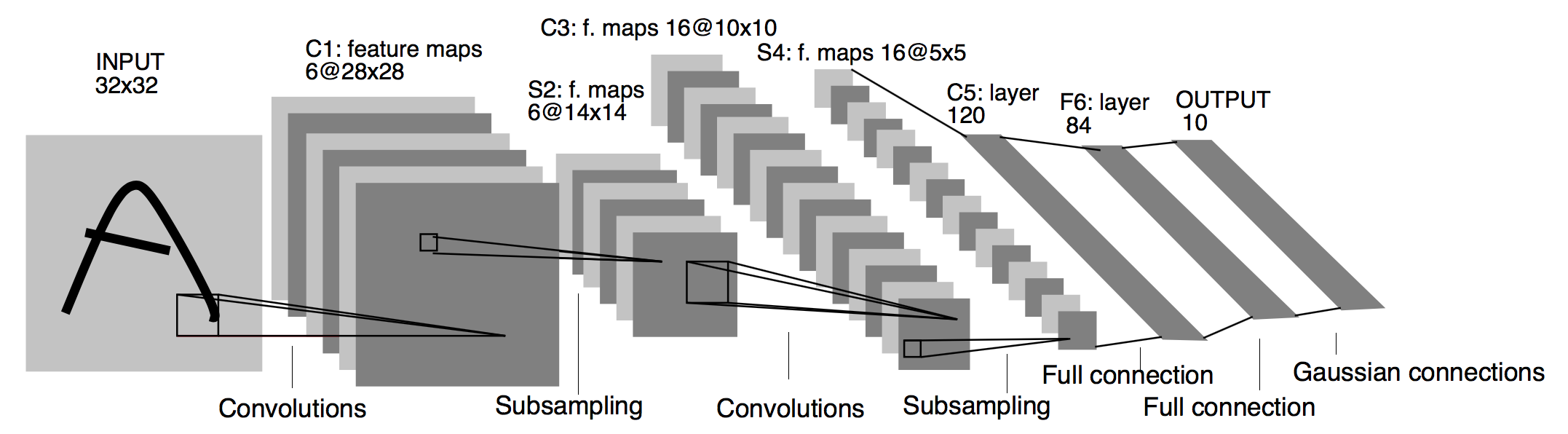
- LeNet分为卷积层块和全连接层块两个部分
- 卷积层块:卷积层+最大池化层,卷积层块由两个这样的基本单位重复堆叠构成,既卷积层+最大池化层+卷积层+最大池化层,输出为形状为 (批量大小, 通道, 高, 宽)
- 卷积层:
- 作用:卷积层用来识别图像里的空间模式,如线条和物体局部
- 卷积核大小:5×5
- 激活函数:sigmoid
- 输入形状:通道数:第一个是6,第二个是16(为什么)
- 卷积层:
- 网络结构
2. 最大池化层:
1. 作用:之后的最大池化层则用来降低卷积层对位置的敏感性
2. 窗口大小:2×2
3. 步幅:2(步幅与窗口大小相同,池化窗口在输入上每次滑动所覆盖的区域互不重叠。)
- 全连接层块:当卷积层块的输出传入全连接层块时,全连接层块会将小批量中每个样本变平(flatten)。也就是说,全连接层的输入形状将变成二维,其中第一维是小批量中的样本,第二维是每个样本变平后的向量表示,且向量长度为通道、高和宽的乘积。
- 全连接层块含3个全连接层。
- 每层的输出个数分别是120、84和10,
- 实现代码
import time import torch from torch import nn, optim import sys sys.path.append("..") import d2lzh_pytorch as d2l device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') class LeNet(nn.Module): def __init__(self): super(LeNet, self).__init__() self.conv = nn.Sequential( nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size nn.Sigmoid(), nn.MaxPool2d(2, 2), # kernel_size, stride nn.Conv2d(6, 16, 5), nn.Sigmoid(), nn.MaxPool2d(2, 2) ) self.fc = nn.Sequential( nn.Linear(16*4*4, 120), nn.Sigmoid(), nn.Linear(120, 84), nn.Sigmoid(), nn.Linear(84, 10) ) def forward(self, img): feature = self.conv(img) output = self.fc(feature.view(img.shape[0], -1)) return output- AlexNet
- 相比LeNet的改进
- 包含更多的层,每层的行踪更大
- 激活函数改变,sigmoid->ReLU函数,更加简单,更容易新南路
- 通过丢弃法控制全连接层的模型复杂度。
- 通过引入大量的图像增广,如翻转、裁剪和颜色变化,从而进一步扩大数据集来缓解过拟合。
- 结构
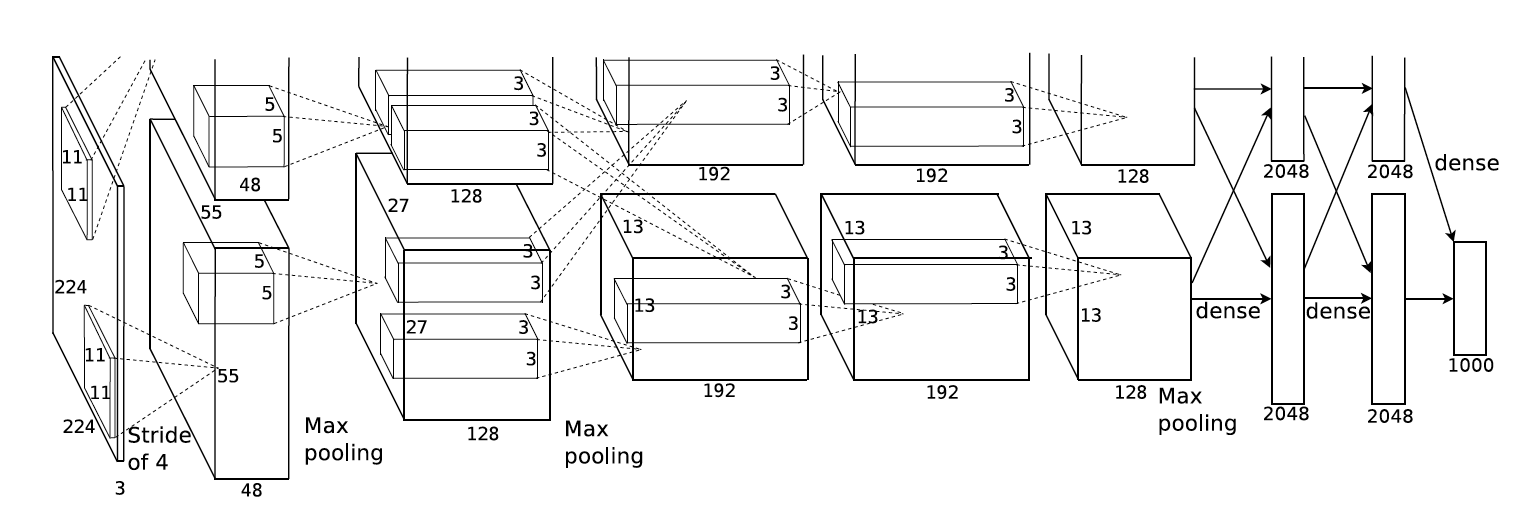
- AlexNet跟LeNet结构类似,但使用了更多的卷积层和更大的参数空间来拟合大规模数据集ImageNet。它是浅层神经网络和深度神经网络的分界线。
- VGG
- NiN
在AlexNet的基础上,NiN去掉了AlexNet最后的3个全连接层,取而代之地,NiN使用了输出通道数等于标签类别数的NiN块,然后使用全局平均池化层对每个通道中所有元素求平均并直接用于分类。这里的全局平均池化层即窗口形状等于输入空间维形状的平均池化层。NiN的这个设计的好处是可以显著减小模型参数尺寸,从而缓解过拟合。然而,该设计有时会造成获得有效模型的训练时间的增加。四、批量归一化
我们对输入数据做了标准化处理:处理后的任意一个特征在数据集中所有样本上的均值为0、标准差为1。标准化处理输入数据使各个特征的分布相近:这往往更容易训练出有效的模型。
我们首先来思考一个问题,为什么神经网络需要对输入做标准化处理?原因在于神经网络本身就是为了学习数据的分布,如果训练集和测试集的分布不同,那么导致学习的神经网络泛化性能大大降低。同时,我们在使用mini-batch对神经网络进行训练时,不同的batch的数据的分布也有可能不同,那么网络就要在每次迭代都去学习适应不同的分布,这样将会大大降低网络的训练速度。因此我们需要对输入数据进行标准化处理。
通常来说,数据标准化预处理对于浅层模型就足够有效了。随着模型训练的进行,当每层中参数更新时,靠近输出层的输出较难出现剧烈变化。但对深层神经网络来说,即使输入数据已做标准化,训练中模型参数的更新依然很容易造成靠近输出层输出的剧烈变化。这种计算数值的不稳定性通常令我们难以训练出有效的深度模型。
(另外一种解释,。。。。。。。。。。。。
网络一旦train起来,那么参数就要发生更新,除了输入层的数据外(因为输入层数据,我们已经人为的为每个样本归一化),后面网络每一层的输入数据分布是一直在发生变化的,因为在训练的时候,前面层训练参数的更新将导致后面层输入数据分布的变化。我们把网络中间层在训练过程中,数据分布的改变称之为:Internal Covariate Shift(输入分布不稳定)。为了解决Internal Covariate Shift,便有了Batch Normalization的诞生。)
批量归一化的提出正是为了应对深度模型训练的挑战。在模型训练时,批量归一化利用小批量上的均值和标准差,不断调整神经网络中间输出,从而使整个神经网络在各层的中间输出的数值更稳定。批量归一化和下一节将要介绍的残差网络为训练和设计深度模型提供了两类重要思路。
批量归一化又叫BN层 - 对全连接层做批量归一化
改变隐藏层,在仿射变换(做y=wx+b运算的那个东西)和激活函数直接,新增加一种计算BN,全连接层的输出改成下面
ϕ(BN(wx+b))
BN大概计算过程是计算均值和方差,然后求元素的平方根和除法进行标准化。
使用库函数nn.BatchNorm1d,可以实现这个操作。这个操作又引入两个新的参数,拉伸参数和偏移参数。net = nn.Sequential( nn.Conv2d(1, 6, 5), # in_channels, out_channels, kernel_size nn.BatchNorm2d(6), nn.Sigmoid(), nn.MaxPool2d(2, 2), # kernel_size, stride nn.Conv2d(6, 16, 5), nn.BatchNorm2d(16), nn.Sigmoid(), nn.MaxPool2d(2, 2), d2l.FlattenLayer(), nn.Linear(16*4*4, 120), nn.BatchNorm1d(120), nn.Sigmoid(), nn.Linear(120, 84), nn.BatchNorm1d(84), nn.Sigmoid(), nn.Linear(84, 10) ) - 卷积层批量归一化
对卷积层来说,批量归一化发生在卷积计算之后、应用激活函数之前。如果卷积计算输出多个通道,我们需要对这些通道的输出分别做批量归一化,且每个通道都拥有独立的拉伸和偏移参数,并均为标量。
使用库函数nn.BatchNorm2d 可以实现这个操作。
在预测阶段,由于训练使用了BN层,所以在预测的时候,也会将BN层的参数加大预测的计算过程中。五、残差网络(ResNet)
解决的问题
在VGG中,卷积网络达到了19层,在GoogLeNet中,网络史无前例的达到了22层。那么,网络的精度会随着网络的层数增多而增多吗?在深度学习中,网络层数增多一般会伴着下面几个问题
计算资源的消耗
模型容易过拟合
梯度消失/梯度爆炸问题的产生
问题1可以通过GPU集群来解决,对于一个企业资源并不是很大的问题;问题2的过拟合通过采集海量数据,并配合Dropout正则化等方法也可以有效避免;问题3通过Batch Normalization也可以避免。貌似我们只要无脑的增加网络的层数,我们就能从此获益,但实验数据给了我们当头一棒。
随着网络层数的增多,训练集loss逐渐下降,然后趋于饱和,当你再增加网络深度的话,训练集loss反而会增大。注意这并不是过拟合,因为在过拟合中训练loss是一直减小的。
当网络退化时,浅层网络能够达到比深层网络更好的训练效果,这时如果我们把低层的特征传到高层,那么效果应该至少不比浅层的网络效果差,或者说如果一个VGG-100网络在第98层使用的是和VGG-16第14层一模一样的特征,那么VGG-100的效果应该会和VGG-16的效果相同。所以,我们可以在VGG-100的98层和14层之间添加一条直接映射(Identity Mapping)来达到此效果。
从信息论的角度讲,由于DPI(数据处理不等式)的存在,在前向传输的过程中,随着层数的加深,Feature Map包含的图像信息会逐层减少,而ResNet的直接映射的加入,保证了 层的网络一定比 层包含更多的图像信息。
基于这种使用直接映射来连接网络不同层直接的思想,残差网络应运而生。
残差网络是参照VGG搭建的。



