本章概念:
一、输入数据处理
网络要处理的文本数据,需要将文本中的每个词都转换成one-hot向量。长度设为d(即为词典的大小)
设输入数据的批次大小为n,步长step,那么每次(每个时间步)计算的时候,都是输入n个字符串,每个字符串的长度是step。
时间步t的输入Xt的形状,转换为[step, n, d]。假设步长为5,batch size 为2,词典大小1027,那么每次输入计算的数据为[5,2,1027]
Q:前几节举例子,输入数据的形状一般为(n,d),这次为什么(step, n, d)?
A:可以理解为,输入数据多了一个维度,类似图形的多通道。
Q:图形多通道数据输入时,输入数据的形状第一个维度是批量大小n,这次为什么是步长step?
A:首先,这不是多层感知机的网络,所以采用不同的形状是可以的。
其次,这样做的好处是,改变字符串长度时,当批量大小和词典大小不变时,网络结构和参数的shape不用改
最后,这样做的改变如下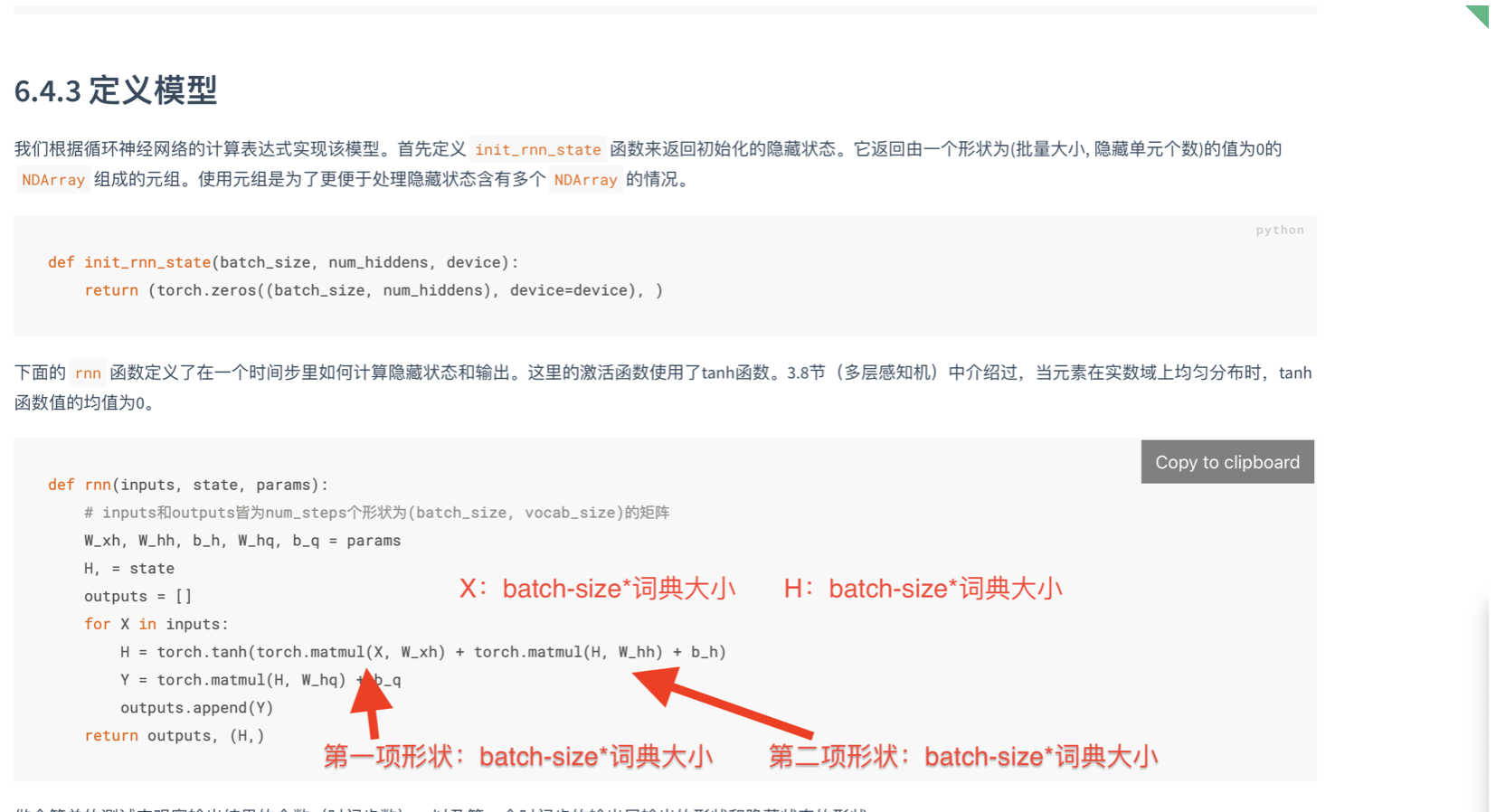
(图片修正:H:batch-size 隐藏单元个数
第一项形状:batch-size 隐藏单元个数,第二项形状:batch-size * 隐藏单元个数。)
二、初始化模型参数
参数在上节讨论隐藏状态时,已经提过。这里主要解释,参数初始化的shape。
Init的作用类似递归函数,需要一个初始值,所以初始值的shape也要保持统一
三、定义模型
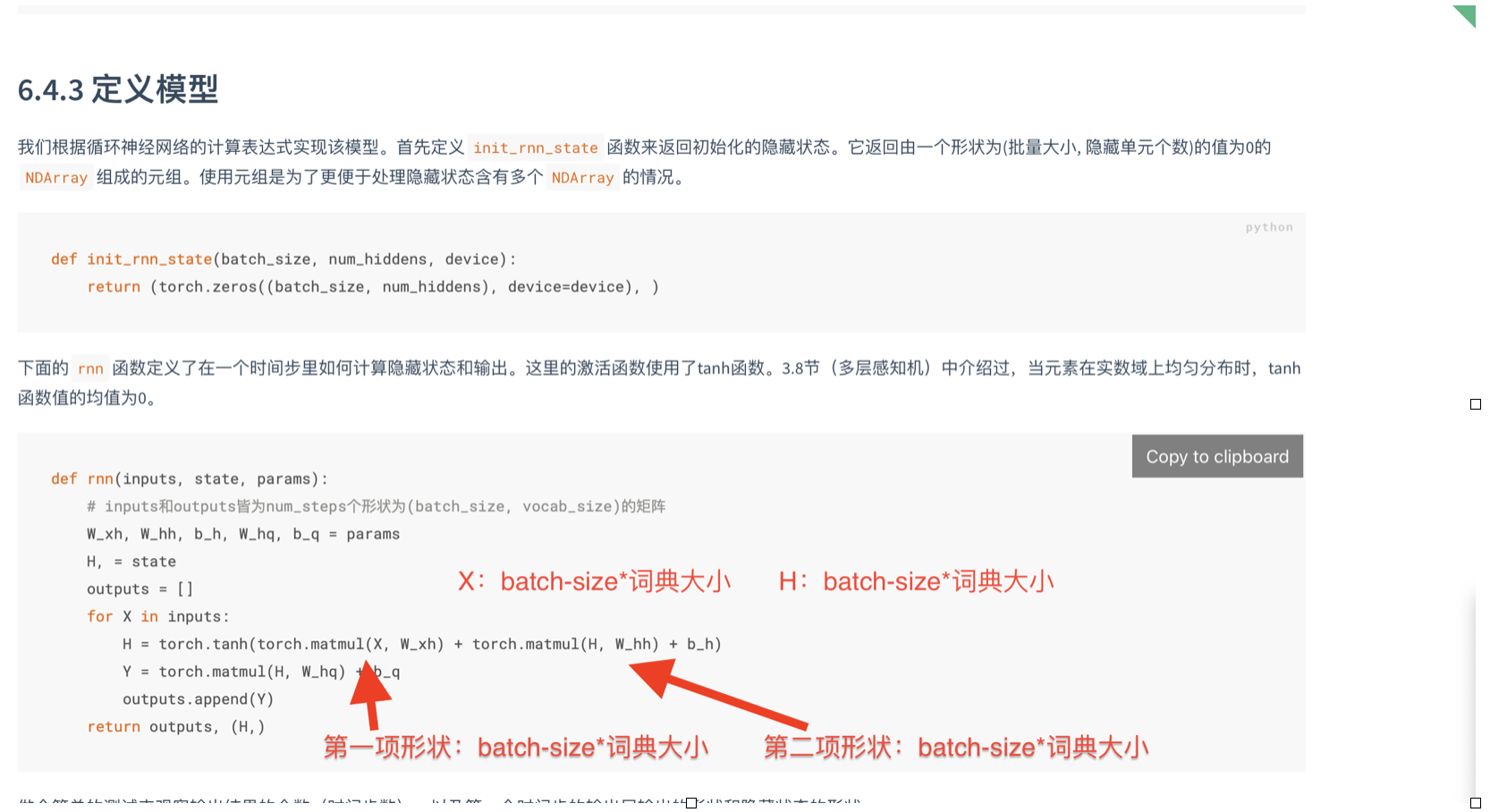
修正:H:batch-size 隐藏单元个数
第一项形状:batch-size 隐藏单元个数,第二项形状:batch-size * 隐藏单元个数。
四、定义预测函数
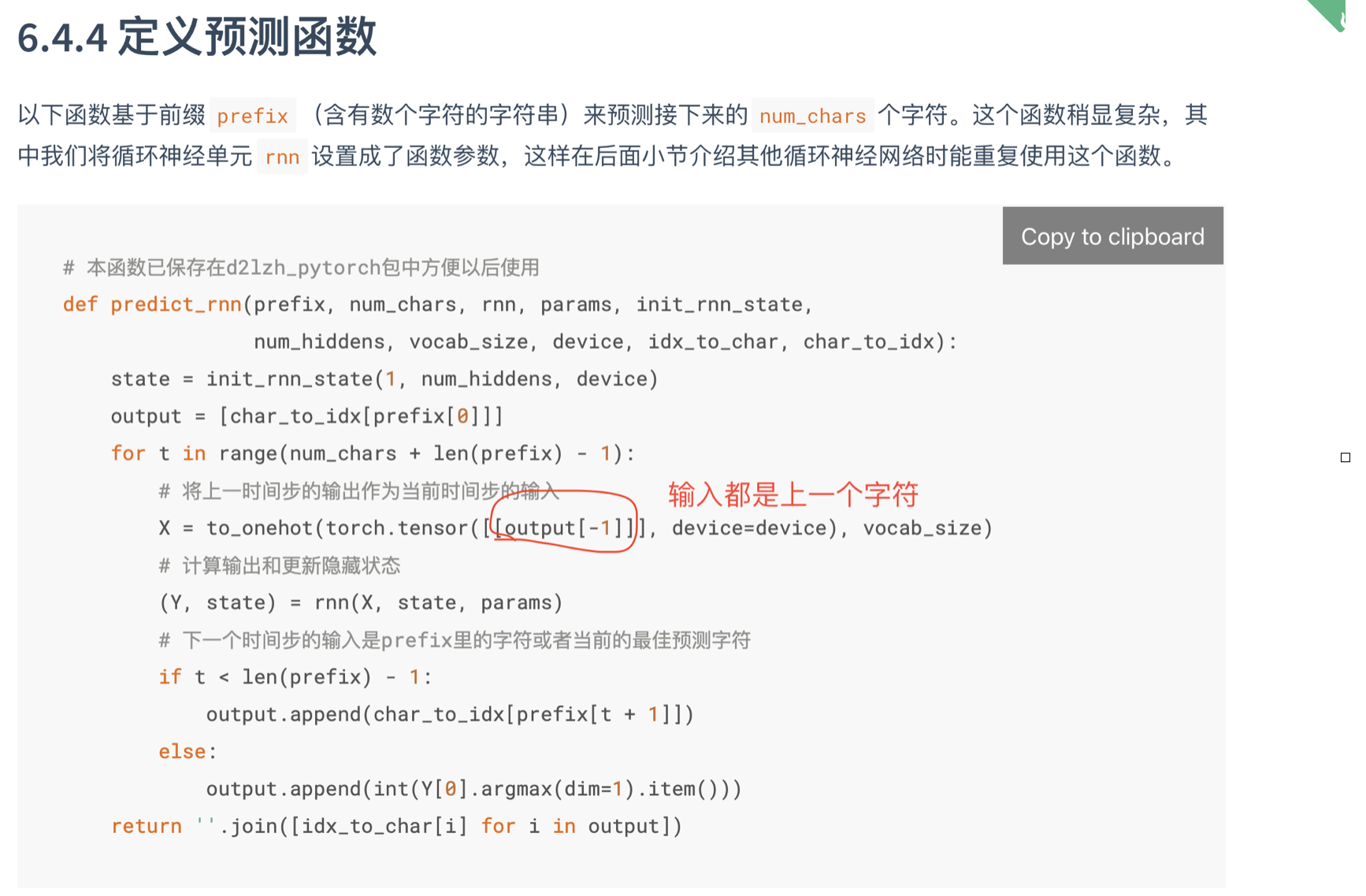
这个函数是基于前缀prefix(一个字符串)来预测接下来的num_chars个字符。里面有个trick,只使用了prefix的第一个字符,后面的预测都是根据这一个字符来计算的,当长度小于prefix时,就不用预测结果,用prefix里面的字符。
五、裁剪梯度
可以理解成,每次计算梯度的时候,都把梯度给缩小了,实现方式就是把参数乘一个系数。
六、使用困惑度评价好坏
最佳情况下,模型总是把标签类别的概率预测为1,此时困惑度为1;
最坏情况下,模型总是把标签类别的概率预测为0,此时困惑度为正无穷;
基线情况下,模型总是预测所有类别的概率都相同,此时困惑度为类别个数。
计算方式是对交叉熵损失函数做指数运算。
七、训练函数
主要是转换预测值和y的shape
八、简洁实现
nn.RNN



