面试必问-Attention为什么要除以$\sqrt{d}$

问题： Attention计算中为什么要除以$\sqrt{d}$?

标准答案

为了避免当d的值较大时，点积结果变得过大。如果不进行这样的缩放处理，过大的点积值会使softmax函数的结果趋向于极端值，进而导致梯度消失的问题，影响模型训练的效果。

那为什么不选择其他数，要选$\sqrt{d}$?

标准答案

因为希望$QK^T$的点积结果期望为0 方差为1，$QK^T$的方差是d， 需要除d的平方根，才能让点积方差为1。

推理和理解（只回答标准答案即可，这部分是为了让你明白为什么有答案）

先说推理过程：
step1：如果d变大，会导致$QK^T$方差会变大。
step2：方差变大会导致元素的差异变大。
step3：元素的差异变大会导致 softmax函数退化为 argmax函数, 也就是经过softmax之后，最大值对应的值为1，其他值则为0。
step4：softmax函数只有一个值为1的元素，其他都为0的话，反向传播的梯度会变为0, 也就是所谓的梯度消失。

接着，我们一步一步的论述上面四个步骤。

论述1：如果d变大，为什么会导致Q$\cdot$K方差会变大？

我们假设查询向量Q和键向量K都是期望为0，方差为1的独立随机变量。
点积的方差$D(QK^T)$计算如下:

$$\begin{aligned} D(QK^T) &=D(\sum_{i=1}^dq_i*k_i)\\ &=\sum_{i=1}^dD(q_i*k_i)\\ &=\sum_{i=1}^dE(q_i^2k_i^2)-[E(q_ik_i)]^2\\ &=\sum_{i=1}^dE(q_i^2)E(k_i^2)-[E(q_i)E(k_i)]\\ &=\sum_{i=1}^d(1*1-0)\\ &=d \end{aligned}$$

所以当d变大时，QK^T的方差变大。

论述2：为什么方差变大，会导致元素之间的差异会变大？

方差（Variance）是统计学中的一个重要概念，用于衡量一组数据的离散程度。具体来说，方差描述了各个数据点与它们的平均值之间的差异大小。
方差的大小可以反映数据的波动程度：
方差越大，表示数据越分散。
方差越小，表示数据越集中。
我们可以从下面的例子看出来，方差和数据分散的程度。
比如

例子 1：数据集 A 和 B

假设有两个数据集 A 和 B，每个数据集包含 5 个数值
数据集 A

$$A = [10, 12, 14, 16, 18]$$

数据集 B

$$B = [8, 10, 14, 18, 20]$$

这两个数据集的期望都是14，方差分别为

$$\begin{aligned} D(A) &= \frac{1}{5-1} \left( (10-14)^2 + (12-14)^2 + (14-14)^2 + (16-14)^2 + (18-14)^2 \right)\\ &= \frac{1}{4} \left( (-4)^2 + (-2)^2 + 0^2 + 2^2 + 4^2 \right)\\ &= \frac{1}{4} \left( 16 + 4 + 0 + 4 + 16 \right) = \frac{40}{4} = 10\\ \end{aligned}$$ $$\begin{aligned} D(B) &= \frac{1}{5-1} \left( (8-14)^2 + (10-14)^2 + (14-14)^2 + (18-14)^2 + (20-14)^2 \right)\\ &= \frac{1}{4} \left( (-6)^2 + (-4)^2 + 0^2 + 4^2 + 6^2 \right)\\ &= \frac{1}{4} \left( 36 + 16 + 0 + 16 + 36 \right) = \frac{104}{4} = 26 \end{aligned}$$

A和B的均值一样，但是B的方差比较大，我们看一下两个数据集的分布。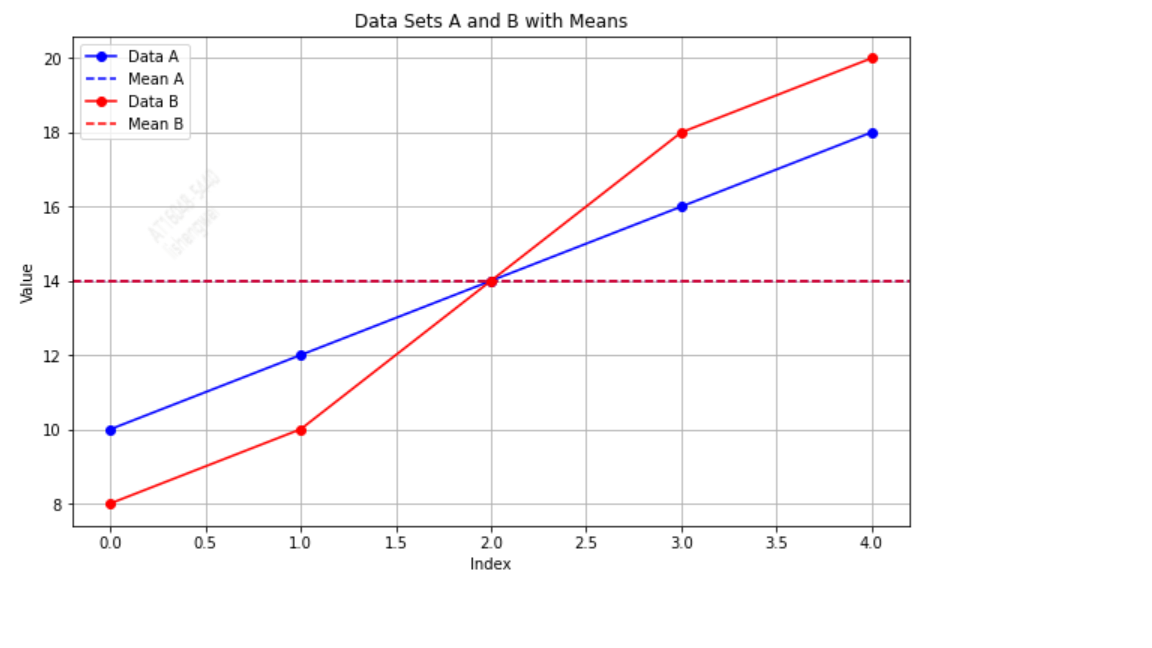

论述3：元素的差异为什么变大会导致softmax函数退化为argmax函数？

softmax会根据每个值进行概率分布，值越大，softmax计算后的概率就会越大，当元素差异比较大时，softmax函数将会趋近于将最大的元素赋值为 1 。
我们可以看个例子。

import numpy as np

n = 10

x1 = np.random.normal(loc=0, scale=1, size=n)
x2 = np.random.normal(loc=0, scale=np.sqrt(512), size=n)
print('x1最大值和最小值的差值:', max(x1) - min(x1))
print('x2最大值和最小值的差值:', max(x2) - min(x2))

def softmax(x):
    return np.exp(x) / np.sum(np.exp(x), keepdims=True)

def softmax_grad(y):
    return np.diag(y) - np.outer(y, y)

ex1 = softmax(x1)
ex2 = softmax(x2)
print('softmax(x1) =', ex1)

print('softmax(x2) =', ex2)

x1最大值和最小值的差值: 3.1926862641908134
x2最大值和最小值的差值: 41.978363005483445
softmax(x1) = [0.01516924 0.06502981 0.05622141 0.22766582 0.07155582 0.28119687
 0.18735697 0.01898374 0.01154634 0.06527397]
softmax(x2) = [0.         0.00001019 0.75357824 0.24640381 0.00000701 0.00000074
 0.         0.         0.         0.        ]

可以看出, 在X2的方差的时候, softmax之后只有第三个元素接近1, 其他都几乎为0。

论述4：softmax函数为什么会导致梯度消失？

在第三步中我们证明了当方差变大的时候, softmax 退化成了 argmax, 也就是变成一个只有一个 1 其他全为 0 的向量。
这个向量带入到上面的雅可比矩阵会发生什么? 我们发现对于任意的y_k=1,y_j<>k=0的向量来说，雅各比矩阵变成了一个全0矩阵。也就是说梯度全为 0了，变成了梯度消失。